
WUWT By John A. Parmentola, The RAND Corporation | Oct. 1, 2022
I have been working on Milankovitch Theory for about three years, trying to understand it. In doing so, I have gained some new insights into this theory. I have also discovered that there are some misconceptions about what it is. This brief note summarizes my work while clarifying several aspects of the theory.
Milankovitch Theory is not a complete theory. It’s more of a hypothesis concerning insolation changes over time and the associated recurrence of ice ages. It is also not a climate model, as some assume. The Milankovitch hypothesis represents a set of insolation conditions on the earth’s climate system; however, the earth’s specific climate response to these conditions is not understood. That is a critical unknown factor relevant to predicting the future state of the earth’s climate.
In his original papers [1], Milutin Milankovitch proposed that the obliquity was a dominant factor in ice age occurrences because it affects the insolation at northern latitudes where ice and snow can accumulate on the earth’s comparatively large landmass of the northern hemisphere. Snow and ice accumulation can affect the earth’s albedo and hence its heat engine. It is likely that the earth’s climate response to changes in insolation at northern latitudes involves the extreme cyclonic weather at the poles primarily caused by the Coriolis Force and the dynamic change in the insolation over periods of roughly 10,000 years. These polar regions are each the size of Asia, containing enormous amounts of cold, dense air that is held in check by the jet stream. However, the specific physical mechanism within these regions that responds to insolation changes over extended periods to cause ice ages remains a mystery.
There are three celestial parameters involved in the earth’s motion, namely, the precession, obliquity, and eccentricity. None of these is periodic, as indicated by the following graphs of the eccentricity, precession, and obliquity half-cycles,

While they are cyclical, each of them has no fixed period. Instead, there are cyclical ranges. They are all quasiperiodic functions of time due to effects from other planets and the sun on the earth’s motion. Therefore, there are no fixed frequencies; however, power spectral density analyses of the paleoclimate data reveal certain characteristic frequencies. These are associated with the three celestial parameters and are used to explain certain recurring features in the paleoclimate data, as indicated by the following graphs associated with Vostok ice core data [2],

The shortest cycle of the three celestial parameters is that of the precession, which, over the last 800,000 years, on average, has been about 21,000 years. That of the obliquity has been about 41,000 years and the eccentricity about 94,000 years. However, the variation in these cycles and their half-cycles is quite large. For example, the half-cycles vary for the precession from 7,000 to 15,000 years, the obliquity from 18,000 to 23,000 years, and the eccentricity from 30,000 to 70,000 years. In terms of timescales, the precession sets the scale for the time-dependent behavior of the insolation. The significant quantity is the precession half-cycle, which is about 11,000 years on average.
The insolation is inherently a wave phenomenon; however, this characterization is not acknowledged in the literature. Think of it as analogous to an AM radio wave. Its wave-like nature occurs from the “beating” of the earth’s celestial motions on the solar irradiance (about 1,368 Watts/m2), which results in its complex time-dependent distribution over the earth’s surface, i.e., the insolation. Each of the three celestial motions contributes a wave component to the insolation. Like ordinary waves, they can constructively and destructively interfere. This description begs several questions. How large in magnitude is each of these wave components, and how do they interfere? Does the interference manifest itself in the paleoclimate data, and how? Does the description of the insolation as a wave and its components have any predictive power? My work sheds some light on these questions.
In terms of physical effects, the obliquity primarily affects the insolation distribution over the earth. Its oscillatory behavior shifts the sun’s rays north and south by about 2.4 degrees in latitude or roughly 140 miles. This shift changes the angle the sun’s rays make with the vertical at each illuminated point on the earth resulting in a comparatively small overall effect on the insolation amplitude.
The most significant effect on the insolation amplitude comes from the combination of the precession and eccentricity, the precession index. It’s defined as the precession modulated by the eccentricity. It accounts for insolation minima and maxima. For example, when the earth is at perihelion, the closest distance to the sun, and the earth’s axis points toward the sun, the insolation approaches a maximum for the northern hemisphere. Fast forward about 11,000 years, an average precession half-cycle, the earth’s axis points toward the sun at aphelion, the farthest distance from the sun, and the insolation approaches a minimum for the northern hemisphere. The change from maximum to minimum and vice versa can be quite significant (more than 100 Watts/m2) at northern latitudes during the summer solstice and is driven by changes in the eccentricity over a precession half-cycle.
Over the last 800,000 years, the insolation has transitioned from maxima to minima and vice versa a total of 74 times; however, the number of prominent interglacial periods indicated in paleoclimate data is at best 13. These features are represented by the following graphs of insolation predictions at 65 degrees north latitude during June [3] and EPICA Dome C ice core data from Antarctica rendered through a temperature model over the last 800,000 years [4].
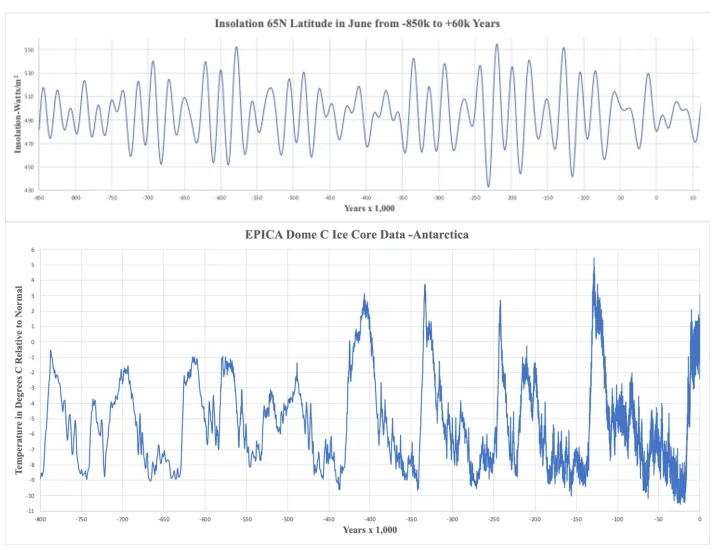
Steep rises and subsequent major temperature declines are comparatively infrequent; however, the timescale of these changes is about 10,000 years, which approximately coincides with the precession half-cycle. What, if any, relationship is there between insolation changes and prominent features in the paleoclimate data? Are there specific insolation changes that are special, or are there trends in the insolation over time that correlate with significant changes in the paleoclimate data? To gain some insight into correlations, one might consider the largest changes in insolation from minimum to maximum and maximum to minimum to see if these influenced the paleoclimate data more than other insolation changes.
Since the obliquity affects the distribution of the solar irradiance over the earth with a comparatively small effect on its amplitude over long periods and the precession index is the primary driver of amplitude variations over shorter periods, the product of the two contributions should well approximate the insolation. This approximation has the added benefit of enabling the partitioning or deconvolution of these two effects in time and allows a time series comparison of the model predictions and the paleoclimate data. In this way, the quasiperiodic nature of the celestial parameters is accounted for explicitly.
Suppose one now calculates the percentage change between maxima and minima and vice versa using this model and interpolates between these extrema. In that case, the result is a complex wave having a beat structure describing the changing trends in the insolation. From the deconvolution model, the obliquity-wave (O-Wave) contribution to the percentage change oscillates quasi-periodically over 800,000 years with a comparatively small amplitude. Over the same period, the precession index contribution to the percentage change takes the form of recurring wave packets (PI-Wave) composed of a precession carrier wave modulated by an eccentricity envelope. The PI wave packet amplitudes, on average, exceed those of the O-Wave by a factor of four, as can be seen by the following graph,

Where the blue curve corresponds to the PI-Wave, the red curve the O-Wave, and the grey curve their total. Therefore, the PI-Wave drives the behavior of the insolation while the O-Wave tends to enhance it through constructive and destructive interference over much longer times scales that are roughly a factor of two greater on average. The sum of the O-Wave and PI-Wave at the extrema points can be shown to have about 1% accuracy based on a comparison with the high-precision insolation computations of Laskar et al. All numerical calculations make use of data generated from this computational tool [2]. The interpolation accuracy between the sparse set of extrema points is unknown.
Because the O-Wave and PI-Wave are time series model predictions, they can be directly compared with paleoclimate time series data. For example, the PI wave packets approximately correlate with the occurrence of interglacial periods, and the temperature trends correlate with the increasing and decreasing PI-Wave amplitudes as indicated by the following graphs,

Note the similarity between the wave packet structure indicated by the vertical lines at the far left and the packet to the far right associated with the Holocene. This similarity enables an estimate of the termination of the current warm period (see below).
From this novel wave description of the insolation, the deconvolution model can account for the following prominent features in the paleoclimate data:
1) The aperiodic recurrence of interglacial-glacial periods over the last 800,000 years approximately coincides with the quasiperiodic PI-Wave;
2) The paleoclimate temperature trends, such as those in the EPICA Dome C data, closely follow rising and declining trends in the PI-Wave contribution to the insolation;
3) All interglacial terminations over the last 800,000 years occur in the same manner through steep declines in the PI-Wave contribution to the insolation enhanced by the O-Wave contribution;
4) The temporal extent of interglacial periods is of two types that are accounted for by the constructive and destructive interference of the O-Wave and PI-Wave contributions to the insolation;
5) and all interglacial inceptions over the last 800,000 years coincide with synchronized constructive interference between the PI-Wave and O-wave contributions to the insolation, except for the timing of two inceptions.
The two inceptions that fail are deep ice cores. However, a detailed temporal comparison of the benthic LR04 data [4] and EPICA Dome C ice core data [3] demonstrate that the most significant timing differences between these data sets coincide with the inception timing disparities from the deconvolution model predictions [6]. This discrepancy suggests that there may be something wrong with the EPICA Dome C ice core data, which is not surprising given its model dependence and the depth of the ice cores.
Finally, through the deconvolution model, interglacial termination periods can be estimated, which all appear to be in the same ballpark in terms of duration. They are all about 11,000 years except for one, Marine Isotope Stage 13c, which is about 15,000 years; however, its greater duration can be understood in terms of the quantitative and qualitative behaviors of the O-Wave and PI-Wave contributions to the insolation.
From the model, the Holocene interglacial will likely terminate within the next 500 years. It’s a low-resolution estimate because the insolation minimum the earth is currently in is very shallow. A very similar interglacial occurred about 787,000 years ago, which terminated in a similar way. The following graphs indicate the shallowness of the Holocene, Marine Isotope Stage 1, and Marine Isotope Stage 19c insolation minima,
The consistency of the deconvolution model with the prominent features of the paleoclimate data suggests a physical description reminiscent of a resonance system; however, proving this is a whole other matter. The following description should be considered speculation or, at best, a hypothesis.
We know from a harmonic oscillator that it is the nature of a resonant system to respond strongly to influences that have frequencies close to its resonant frequency. If a complex, exciting force is applied, such as one having many frequencies, then the system will pick out the components close to its resonant frequency.
For the sun-earth system, the solar irradiance undergoes small percentage changes over time and is evenly distributed along a plane perpendicular to the sun’s rays. The earth’s shape and celestial mechanical motions beat on the solar irradiance with multiple frequencies in a quasiperiodic manner to transform it into the insolation over the earth’s surface. The beating effect is a consequence of gravitational forces on the earth that deviate from a 1/R2 central force law due to the sun, other planets, and its unsymmetrical mass distribution.
This “beating” causes quasiperiodic trends in the insolation primarily due to the precession index (the precession modulated by the eccentricity). The eccentricity through the precession index has amplified and reduced the insolation in a quasiperiodic manner over the last 800,000 years. The climate system’s response to this aperiodic “beating” is quasiperiodic interglacial periods, a resonance response. Simply put, the earth is a sensor that detects and responds to the fundamental rhythms of the solar system.
The interglacial periods are initiated by amplification and terminated by reduction of the insolation due to the eccentricity through the precession index. This effect takes the form of quasiperiodic wave packets with a precession carrier wave modulated by the eccentricity, which accounts for the quasiperiodic recurrence of interglacial-glacial periods. The role of the quasiperiodic obliquity contribution to the insolation is to enhance and diminish the dominant effect of precession index wave packets in initiating and terminating interglacial periods.
That’s it in a nutshell.
About the author
John Parmentola has a Ph.D. in theoretical physics from the Massachusetts Institute of Technology. He has built a highly distinguished career over four decades as an entrepreneur, inventor, innovator, a pioneer in the founding of new fields of research, and leader of complex research and development organizations with broad experience in the private sector, academia, and high-level positions within the federal government and defense community.
Currently, he is a consultant to one of the world’s leading think tanks, The RAND Corporation, where he works on defense, energy, and science and technology assessment, strategy, and planning issues for domestic and foreign government agencies. He also does volunteer work for the National Academy of Sciences.
References
[1] Milankovitch, M.M., 1941. Kanon der Erdbestrahlung und seine Anwendung auf das Eiszeitenproblem. Royal Serbian Sciences, Spec. pub. 132, Section of Mathematical and Natural Sciences, 33, Belgrade, 633 pp., also available in English at https://www.amazon.com/Insolation-Ice-Age-Problem-Milankovic-Milankovitch/dp/8617066199, 1998.
[2] (Petit, J., Jouzel, J., Raynaud, D. et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 399, pp. 429–436, https://doi.org/10.1038/20859, 1999.
[3] J. Laskar et al., IMCCE, Virtual Observatory Solar System Portal, CNRS Observatory, Paris, http://vo.imcce.fr/insola/earth/online/earth/online/index.php, 2018.
[4] NCEI, EPICA Dome C – 800KYr Deuterium Data and Temperature Estimates, https://www.ncei.noaa.gov/access/paleo-search/study/6080, 2007.
[5] Lisiecki, LE. and Raymo, M.E., A Pliocene-Pleistocene Stack of 57 Distributed Benthic d18O Records, AGU Paleoceanography and Paleoclimatology, Vol. 20 (PA1003), pp.1-17, https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/2004PA001071, 2005.
[6] See figure 3, Parrenin, F. et al., The EDC3 Chronology for the EPICA Dome C Ice Core, Clim. Past., Vol. 3, pp. 485-497, Figure 3, pp. 491, https://cp.copernicus.org/articles/3/485/2007/, 2007.




