Abstract
The United Nations Intergovernmental Panel on Climate Change (IPCC) agrees human CO2 is only 5 percent and natural CO2 is 95 percent of the CO2 inflow into the atmosphere. The ratio of human to natural CO2 in the atmosphere must equal the ratio of the inflows. Yet IPCC claims human CO2 has caused all the rise in atmospheric CO2 above 280 ppm, which is now 130 ppm or 32 percent of today’s atmospheric CO2.
To cause the human 5 percent to become 32 percent in the atmosphere, the IPCC model treats human and natural CO2 differently, which is impossible because the molecules are identical. IPCC’s Bern model artificially traps human CO2 in the atmosphere while it lets natural CO2 flow freely out of the atmosphere.
By contrast, a simple Physics Model treats all CO2 molecules the same, as it should, and shows how CO2 flows through the atmosphere and produces a balance level where outflow equals inflow. Thereafter, if inflow is constant, level remains constant.
The Physics Model has only one hypothesis, that outflow is proportional to level. The Physics Model exactly replicates the 14C data from 1970 to 2014 with only two physical parameters: balance level and e-time. The 14C data trace how CO2 flows out of the atmosphere.
The Physics Model shows the 14CO2 e-time is a constant 16.5 years. Other data show e-time for 12CO2 is about 4 to 5 years. IPCC claims human CO2 reduces ocean buffer capacity. But that would increase e-time. The constant e-time proves IPCC’s claim is false.
IPCC argues that the human-caused reduction of 14C and 13C in the atmosphere prove human CO2 causes all the increase in atmospheric CO2. However, numbers show these isotope data support the Physics Model and reject the IPCC model.
The Physics Model shows how inflows of human and natural CO2 into the atmosphere set balance levels proportional to their inflows. Each balance level remains constant if its inflow remains constant. Continued constant CO2 emissions do not add more CO2 to the atmosphere. No CO2 accumulates in the atmosphere.
Present human CO2 inflow produces a balance level of about 18 ppm. Present natural CO2 inflow produces a balance level of about 392 ppm. Human CO2 is insignificant to the increase of CO2 in the atmosphere. Increased natural CO2 inflow has increased the level of CO2 in the atmosphere.
Keywords: carbon dioxide, CO2, climate change, anthropogenic
1. Introduction
The U.S. Global Change Research Program Climate Science Special Report (USGCRP) [1] claims,
This assessment concludes, based on extensive evidence, that it is extremely likely that human activities, especially emissions of greenhouse gases, are the dominant cause of the observed warming since the mid-20th century.
The United Nations Intergovernmental Panel on Climate Change (IPCC) [2] Executive Summary claims human emissions caused atmospheric CO2 to increase from 280 ppm in 1750, to 410 ppm in 2018, for a total increase of 130 ppm.
IPCC and USGCRP claim there are “no convincing alternative explanations” other than their theory to explain the “observational evidence.”
This paper presents a “convincing alternative explanation” that properly explains the data. The Physics Model explains the required first step of human-caused climate change: how human CO2 changes atmospheric CO2.
For simplicity, this paper uses levels in units of ppm (parts per million by volume in dry air) and flows in units of ppm per year. GtC (Gigatons of Carbon) units are converted into CO2 units in ppm using:
1 ppm = 2.12 GtC
Authors who support the USGCRP [1] and IPCC [2, 3] include Archer et al. [4], Cawley [5], Kern and Leuenberger [6], and Kohler [7].
Authors who conclude human CO2 increases atmospheric CO2 as a percentage of its inflow include Revelle and Suess [8], Starr [9], Segalstad [10], Jaworoski [11, 12], Beck [13], Rorsch, Courtney, and Thoenes [14], Courtney [15], Quirk [16], Essenhigh [17], Glassman [18], Salby [19-22], Humlum [23], Harde [24, 25], and Berry [26, 27].
2. The Science Problem
IPCC [2, 3] says nature emits about 120 GtC from land and 90 GtC from ocean for a total of 210 GtC per year. This is equivalent to about 98 ppm per year of natural CO2 that flows into the atmosphere. IPCC admits its estimates of “gross fluxes generally have uncertainties of more than ±20%.”
Boden [28] shows human CO2 emissions in 2014 were 9.7 GTC per year, or 4.6 ppm per year. So, IPCC agrees that human inflow is less than 5% and nature is more than 95% of the total CO2 inflow into the atmosphere. Yet IPCC assumes nature stayed constant since 1750 and human CO2 causes 100 percent the increase in atmospheric CO2 above 280 ppm, which today is 130 ppm or 32 percent of 410 ppm.
The Physics Model concludes the percent of human CO2 in the atmosphere equals the percent of human CO2 in the inflow.
Figure 1 shows how the predictions of the Physics Model and IPCC model differ regarding the composition of human CO2 in the atmosphere.
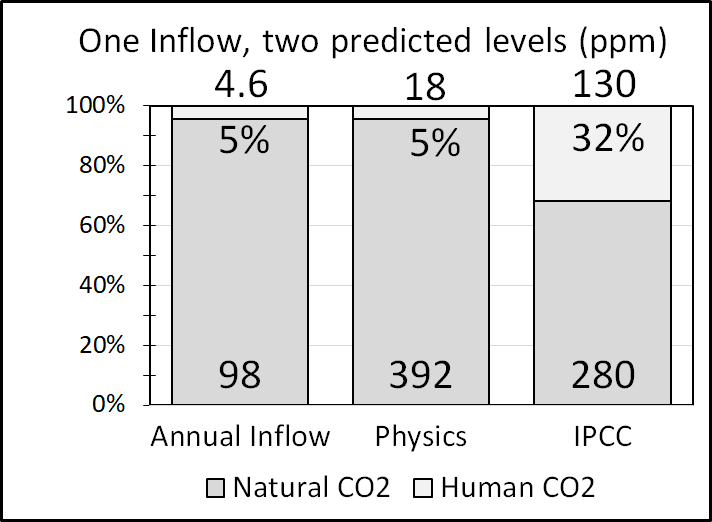
If the IPCC model is correct, then the effect of human CO2 emissions on atmospheric CO2 is 100 percent and the IPCC is correct about human-caused climate change.
If the Physics Model is correct, then human CO2 emissions do not cause climate change.
3. The Physics Model
3.1 How CO2 flows through the atmosphere
IPCC states, and much of the public believes, human emissions “add” CO2 to the atmosphere. IPCC’s view is the atmosphere is a garbage dump where human CO2 is deposited and mostly stays forever.
However, nature must treat human and natural CO2 the same because their molecules are identical. Nature has had millions of years to “add” to atmospheric CO2. If nature’s CO2 “adds” to atmospheric CO2, the CO2 in the atmosphere would be much higher than it is today.
Therefore, natural and human CO2 do not “add” CO2 to the atmosphere. Both natural and human CO2 “flow through” the atmosphere. As CO2 flows through the atmosphere, it raises the level of atmospheric CO2 just enough so CO2 outflow equals CO2 inflow. Nature balances CO2 in the atmosphere when outflow equals inflow.
You pump air into a tire or inner tube that has a leak. As you pump air into the tube, air leaks out of the tube. The faster you pump air in, the faster air leaks out. If you pump air into the tube at a constant rate, the air pressure in the tube will find a level where outflow equals inflow.
River water flows into a lake or a pond and flows out over a dam. If inflow increases, the water level increases until outflow over the dam equals inflow from the river. Then, the water level will remain constant so long as inflow remains constant. The river does not “add” water to the lake. Water “flows through” the lake and finds a balance level where outflow equals inflow.
Similarly, human and natural CO2 flow through the atmosphere. The inflow creates a balance level that remains constant so long as inflow remains constant.
3.2 Physics Model system description
Figure 2 shows a bucket of water as an analogy to CO2 in the atmosphere. Water flows into the bucket at the top and flows out through a hole in the bottom. An outside source (faucet) controls the inflow.
The water level and the hole size control the outflow. No matter what the inflow, the level and the size of the hole control the outflow. Inflow only serves to set a balance level.
This paper uses e-time rather than “residence” time because there are many definitions of residence time. E-time has a precise definition: the time for the level to move (1 – 1/e) of the distance from its present level to its balance level. The balance level is defined below.
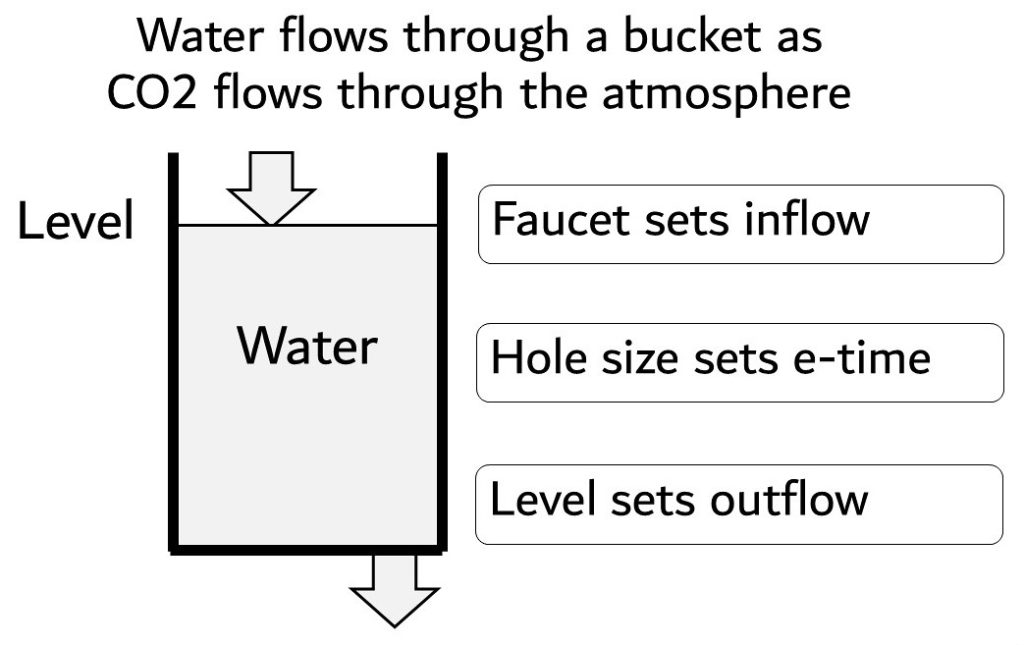
The bucket analogy provides insight into e-time. If the hole in the bucket gets smaller, e-time increases. If the hole in the bucket gets larger, e-time decreases. The hole is an analogy to the ability of the oceans and land to absorb CO2 from the atmosphere.
Figure 3 shows the Physics Model system for atmospheric CO2. The system includes the level (concentration) of CO2 in the atmosphere and the inflow and outflow of CO2.
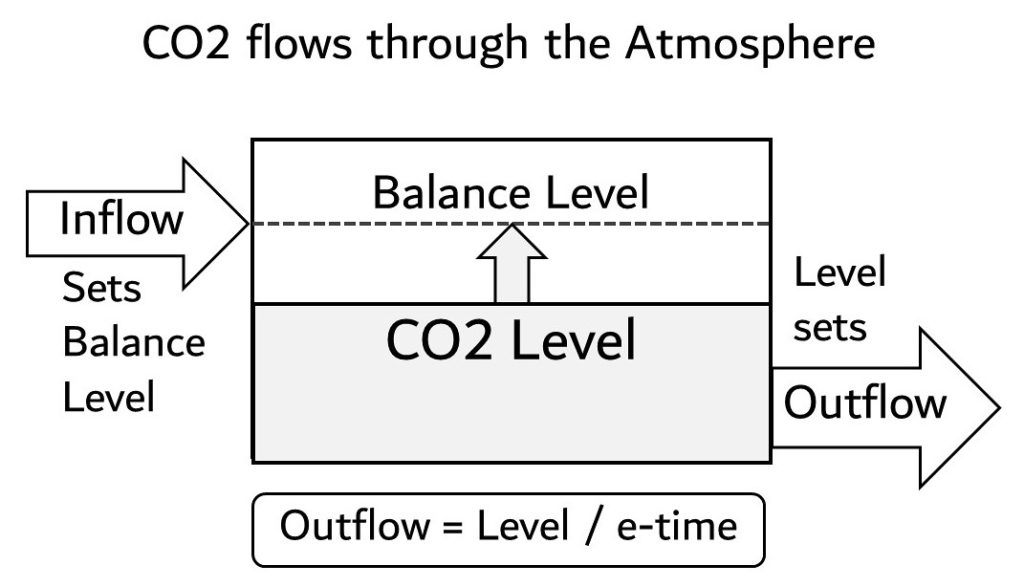
The Physics Model applies independently and in total to all definitions of CO2, e.g., to human CO2, natural CO2, and their sums, and to 12CO2, 13CO2, and 14CO2, and their sums.
The Physics Model is complete. It is not necessary to add separate inflows for human and natural CO2 to the Physics Model. Just use a copy of the Physics Model for each CO2 definition desired.
The Physics Model does not need to describe the details of the external processes. Inflow, outflow, and e-time include all the effects of outside processes. If the Physics Model were connected to land and ocean reservoirs, it would behave exactly as derived in this paper.
Kohler [7] claims Harde’s [24] model and therefore the Physics Model is “too simplistic” and “leads to flawed results for anthropogenic carbon in the atmosphere.”
Kohler is wrong. There is no such thing as a system being “too simplistic.” A system should be as simple as possible to solve a problem. The Physics Model shows how inflow, outflow, and e-time affect the level of CO2 in the atmosphere. The IPCC model cannot do this.
3.3 Physics Model derivation
A system describes a subset of nature. A system includes levels and flows between levels. Levels set flows and flows set new levels. The mathematics used in the Physics Model are analogous to the mathematics used to describe many engineering systems.
The Physics Model derivation begins with the continuity equation (1) which says the rate of change of level is the difference between inflow and outflow:
dL/dt = Inflow – Outflow (1)
Where
L = CO2 level (concentration in ppm)
t = time (years)
dL/dt = rate of change of L (ppm/year)
Inflow = rate CO2 moves into the system (ppm/year)
Outflow = rate CO2 moves out of the system (ppm/year)
Following the idea from the bucket of water, the Physics Model has only one hypothesis, that outflow is proportional to level:
Outflow = L / Te (2)
where Te is the “e-folding time” or simply “e-time.”
Substitute (2) into (1) to get,
dL/dt = Inflow – L / Te (3)
One way to replace Inflow in (3) is to set dL/dt to zero, which means the level is constant. Then Inflow will equal a balance level, Lb, divided by e-time. However, a more elegant way to replace Inflow is to simply define the balance level, Lb, as
Lb = Inflow * Te (4)
Equation (4) shows how Inflow and Te set the balance level. Substitute (4) for Inflow into (3) to get,
dL/dt = – (L – Lb) / Te (5)
Equation (5) shows the level always moves toward its balance level. At this point, both L and Lb are functions of time. Te can also be a function of time.
In the special case when Lb and Te are constant, there is an analytic solution to (5). Rearrange (5) to get
dL / (L – Lb) = – dt / Te (6)
Then integrate (6) from Lo to L on the left side, and from 0 to t on the right side [29] to get
Ln [(L – Lb) / (Lo – Lb)] = – t / Te (7)
where
Lo = Level at time zero (t = 0)
Lb = the balance level for a given inflow and Te
Te = time for L to move (1 – 1/e) from L to Lb
e = 2.7183
The original integration of (6) contains two absolute values, but they cancel each other because both L and Lo are always either above or below Lb.
Raise e to the power of each side of (7), to get the level as a function of time:
L(t) = Lb + (Lo – Lb) exp(– t/Te) (8)
Equation (8) is the analytic solution of (5) when Lb and Te are constant.
The hypothesis (2) that outflow is proportional to level creates a “balance level.” Equation (4) defines the balance level in terms of inflow and e-time.
Figure 4 shows how the level always moves toward its balance level according to (5). While outflow is always proportional to level, inflow sets the balance level.
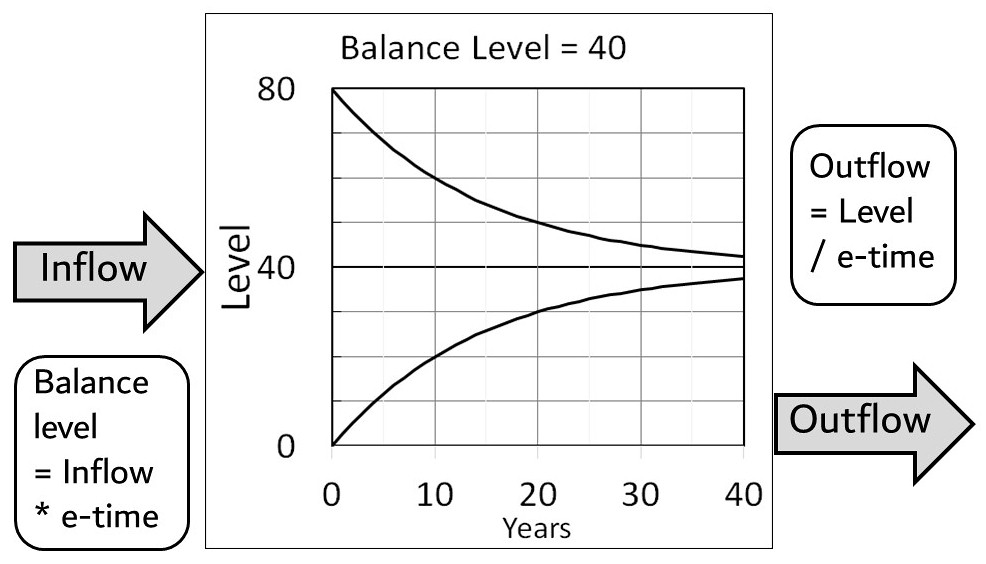
The Physics Model shows how CO2 flows through the atmosphere. CO2 does not “stick” in the atmosphere. A higher inflow merely raises the balance level. Then the level will rise until outflow equals inflow, which will be at the balance level.
3.4 Physics Model consequences
All equations after (2) are deductions from hypothesis (2) and the continuity equation (1).
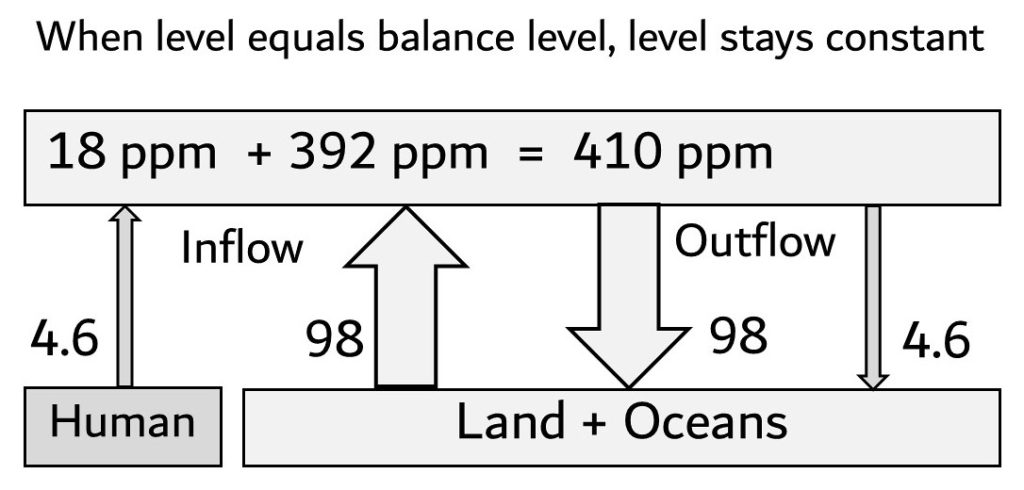
Equation (4) shows the balance level equals the product of inflow and e-time. Using IPCC numbers, and subscripts “p” to mean human (or people) and “n” to mean natural, the balance levels of human and natural CO2 are 18.4 and 392 ppm:
Lbp = 4.6 (ppm/year) * 4 (years) = 18.4 ppm (9)
Lbn = 98 (ppm/year) * 4 (years) = 392 ppm (10)
The ratio of human to natural CO2 is 4.6%. The percentage of human CO2 to total CO2 is 4.5%. Both are independent of e-time:
Lbp / Lbn = 4.6 / 98 = 4.6% (11)
Lbp / (Lbn + Lbp) = 4.6 / 102.6 = 4.5% (12)
Equation (9) shows present human emissions create a balance level of 18 ppm, independent of nature’s balance level. If nature’s balance level remained at 280 ppm after 1750, then present human emissions would have increased the CO2 level 18 ppm from 280 ppm to 298 ppm.
Equation (10) shows present natural emissions create a balance level of 392 ppm. The human contribution of 18 ppm brings the total balance level to 410 ppm, which is close to the level in 2018.
Equation (11) shows the ratio of human to natural CO2 in the atmosphere equals the ratio of their inflows, independent of e-time.
Equation (12) shows the percentage of human-produced CO2 in the atmosphere equals its percentage of its inflow, independent of e-time.
Figure 5 illustrates these Physics Model conclusions when e-time is 4 years.
Equations (9) and (10) support the key conclusions of Harde [24, 25]:
Under present conditions, the natural emissions contribute 373 ppm and anthropogenic emissions 17 ppm to the total concentration of 390 ppm (2012).
4. The IPCC Bern model
4.1 IPCC Bern model origin
In 1992, Siegenthaler and Joos [30] created the original Bern model. Their Figure 1 connects the atmosphere level to the upper ocean level, and the upper ocean level to the deep and interior ocean levels. They used 14C data to trace the flow of 12CO2 from the atmosphere to the upper ocean and to the deep and interior oceans. Using some physics constraints, they attempted without success to fit three versions of their model to available data.
Earlier, in 1987, Maier-Reimer and Hasselmann [31] used an ocean circulation model connected to a one-layer atmosphere to reproduce the main features of the CO2 distribution in the surface ocean. They applied a mathematical curve fit to represent their conclusions. Their curve fit used a sum of four exponentials with different amplitudes and time constants, as in today’s Bern model.
The use of four exponentials by [31] seems to result from their reconnection of both the deep and interior ocean levels directly to the atmosphere level. Such reconnection would be a serious modelling mistake. Other papers followed the model developed by [31].
Archer et al. [4] found the four-exponential models “agreed that 20–35% of the CO2 remains in the atmosphere after equilibration with the ocean (2–20 centuries).”
Joos et al. [32] compared the response of such atmosphere-ocean models to a pulse emission of human CO2. All the models predicted a “substantial fraction” of pulse would remain in the atmosphere and ocean for millennia.
The conclusions of [4, 30, 31, 32] must be questioned because:
- Agreement among models does not prove they are accurate.
- All models treat human and natural CO2 differently, which violates physics.
- All models assume human CO2 causes all the increase in atmospheric CO2, which violates physics.
- All models partition human CO2 inflow into four artificial bins, which is unphysical.
- All models lack a valid physics model for atmospheric CO2.
Segalstad [10] notes that the models like [31] do not allow CO2 to flow out of the atmosphere in linear proportion to the CO2 level. Rather they use a non-linear constraint on the outflow that contradicts physics and chemistry.
Segalstad [10] concludes the alleged long residence time of 500 years for carbon to diffuse to the deep ocean is inaccurate because the 1000 GtC of suspended organic carbon in the upper 75 meters of the ocean can sink to the deep ocean in less than one year. That gives a residence time of 5 years rather than 500 years.
The IPCC Bern model that evolved from models like [31] artificially partitions human CO2 into four separate bins. The separate bins prevent human CO2 in one bin from moving to a bin with a faster e-time. This is like having three holes of different sizes in the bottom of a bucket and claiming the smallest hole restricts the flow through the largest hole.
The IPCC Bern model is unphysical. It begins with the assumption that human CO2 causes all the increase in atmospheric CO2. Then it creates a model that supports this assumption.
The Bern model fails Occam’s Razor because it is unnecessarily complicated.
4.2 IPCC Bern model derivation
The Joos [33] Bern model is an integral equation rather than a level equation.
It is necessary to peer inside IPCC’s Bern model. To deconstruct the integral version of the Bern model, let inflow occur only in the year when “t-prime” equals zero. Then the integral disappears, and the Bern model becomes a level equation.
The Bern level equation is,
L(t) = Lo [ A0 + A1 exp(– t/T1) + A2 exp(– t/T2) + A3 exp(– t/T3)] (13)
Where
t = time in years
Lo = level of atmospheric CO2 in year t = 0
L(t) = level of atmospheric CO2 in year t
and the Bern TAR standard values, derived from curve-fitting the Bern model to the output of climate models, are,
A0 = 0.150
A1 = 0.252
A2 = 0.279
A3 = 0.319
T1 = 173 years
T2 = 18.5 years
T3 = 1.19 years
The A-values weight the four terms on the right-hand side of (13):
A0 + A1 + A2 + A3 = 1.000
In (13), set t equal to infinity to get,
L = A0 Lo = 0.152 Lo (14)
Equation (14) predicts a one-year inflow that sets Lo to 100 ppm, followed by zero inflow forever, will cause a permanent level of 15 ppm.
The four terms in (13) separate human (but not natural) CO2 into 4 bins. Each bin has a different e-time. Only one bin allows human CO2 to flow freely out of the atmosphere. Two bins trap human CO2 for long times. One bin has no outflow and traps human CO2 forever.
Figure 6 shows the size of the four Bern-model bins in percent and the amount of human CO2 that remains in the atmosphere 8 years after an artificial pulse of human CO2 enters the atmosphere.
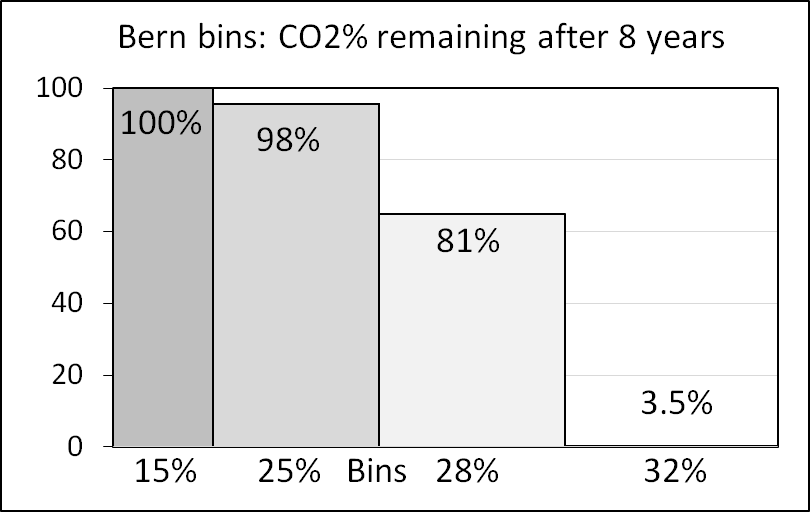
Bern (13) predicts 15 percent all human CO2 entering the atmosphere stays in the atmosphere forever, 25 percent stays in the atmosphere almost forever, and only 32 percent flows freely out of the atmosphere.
4.3 How IPCC gets 32 percent
The burden of proof is upon the IPCC to explain how 5 percent human inflow becomes 32 percent in the atmosphere. IPCC cannot change the inflow. Therefore, IPCC must change the outflow. The IPCC Bern model restricts the outflow of human CO2 while it lets natural CO2 flow freely out of the atmosphere. The IPCC Bern model incorrectly treats human CO2 differently than it treats natural CO2. By doing so, it artificially increases human CO2 in the atmosphere to 32 percent and beyond.
IPCC assumes its Bern model applies to human but not to natural CO2. That assumption is unphysical because CO2 molecules from human and natural sources are identical. All valid models must treat human and natural CO2 the same.
If applied to natural CO2, the Bern model predicts 15 percent of natural CO2 sticks in the atmosphere. Then in 100 years, 1500 ppm of natural CO2 sticks in the atmosphere. This clearly has not happened. Therefore, the Bern model is invalid.
For you mathematicians:
It is simple to prove the Bern model is unphysical. Take the derivative of (13) with respect to time. It is impossible to get rid of the exponential terms because the Bern model has more than one time constant in its exponentials. The Bern model dL/dt does not correspond to a physics formulation of a problem.
By contrast, it is straightforward to take the time derivative of the Physics Model (8) and reproduce its dL/dt form of (5).
The Physics Model began as a rate equation, as all physics models should. The Bern model began with a curve fit to an imaginary scenario for a level rather than as a rate equation for a level. The Bern model does not even include a continuity equation.
5. Theories must replicate data
5.1 The 14C data
The above-ground atomic bomb tests in the 1950s and 1960s almost doubled the concentration of 14C in the atmosphere. The 14C atoms were in the form of CO2, called 14CO2.
After the cessation of the bomb tests in 1963, the concentration of 14CO2 decreased toward its natural balance level. The decrease occurred because the bomb-caused 14C inflow became zero while the natural 14C inflow continued.
The 14C data are in units of D14C per mil. The lower bound in D14C units is -1000. This value corresponds to zero 14C inflow into the atmosphere. In D14C units, the “natural” balance level, defined by the average measured level before 1950, is zero, 1000 up from -1000. [34].
Hua [34] processed 14C data for both hemispheres from 1954 to 2010. Turnbull [35] processed 14C data for Wellington, New Zealand, from 1954 to 2014. After 1970, 14CO2 were well mixed between the hemispheres and 14CO2 in the stratosphere were in the troposphere. The 14C data from both sources are virtually identical after 1970.
14C is an isotope of 12C. Levin et al. [36] conclude the C14 data provide “an invaluable tracer to gain insight into the carbon cycle dynamics.”
5.2 Physics Model replicates the 14C data
The Physics Model (8) accurately replicates the 14CO2 data from 1970 to 2014 with e-time set to 16.5 years, balance level set to zero, and starting level set to the D14C level in 1970.
Figure 7 shows how the Physics Model replicates the 14C data.
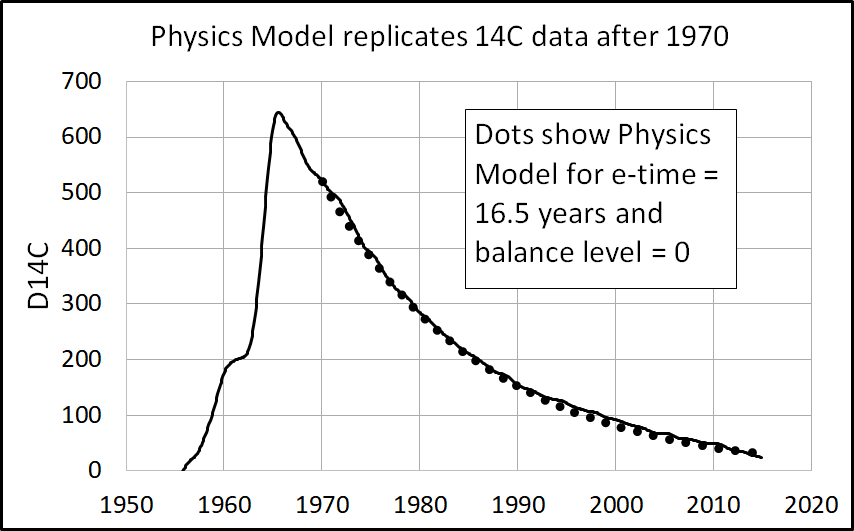
The Physics Model is not a curve fit with many parameters like the Bern model. The Physics model allows only 2 parameters to be adjusted: balance level and e-time, and they are both physical parameters. It is possible that the data would not allow replication by the Physics Model.
The replication of the 14C data begins by setting the Physics Model to the first data point in 1970. Then it is a matter of trying different balance levels and e-times until the model best fits the data. Although there is room for minor differences in the fit, the best fit seems to occur when the balance level is zero and e-time is 16.5 years.
The replication of the 14C data by the Physics Model has significant consequences. It shows the 14C natural balance level has remained close to zero and e-time has remained constant since 1970. If the e-time had changed since 1970, it would have required a variable e-time to make the Physics Model fit the data.
5.3. 12CO2 reacts faster than 14CO2
Isotopes undergo the same chemical reactions but the rates that isotopes react can differ. Lighter isotopes form weaker chemical bonds and react faster than heavier isotopes [37].
Because 12CO2 is a lighter molecule than 14CO2, it reacts faster than 14CO2. Therefore, its e-time will be shorter than for 14CO2.
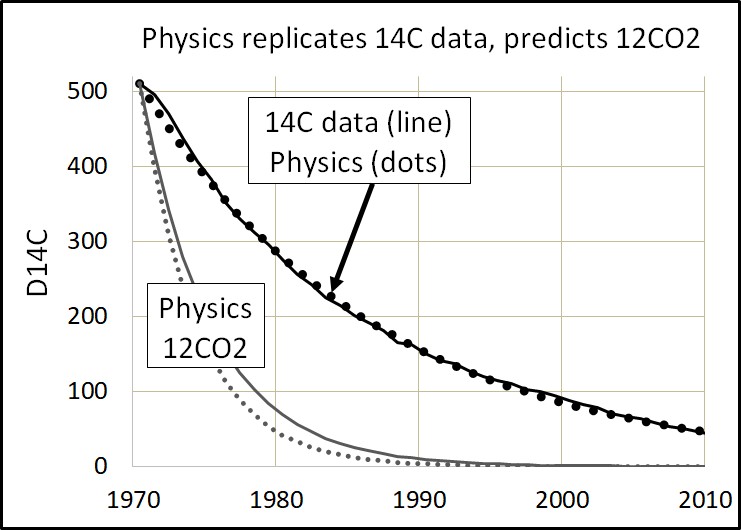
Equation (4) shows e-time equals Level divided by Inflow. Using IPCC numbers, e-time for 12CO2 is about 400 ppm divided by 100 ppm per year, or 4 years. Also, IPCC [3] agrees 12CO2 turnover time (e-time) is about 4 years. Segalstad [10] calculated 5 years for e-time.
Figure 8 shows the Physics Model (8) simulation of 12CO2 using an e-time of 4 years. For comparison, Figure 8 shows the 14C data from Hua [34] and the Physics Model replication of 14CO2 data with an e-time of 16.5.
5.4 IPCC model cannot simulate 12CO2
The Bern model claims to predict the outflow of 12CO2. Therefore, the Bern model should come close to predicting the outflow of 12CO2 as calculated by the Physics Model that replicates the 14C data.
Figure 9 shows the Bern model (13) predictions. The IPCC Bern model begins with a short e-time, then increases its e-time. The increased e-time causes the Bern line to cross the 14C line and thus conflicts with the 14C data. The Bern model traps 15 percent of human CO2 in the atmosphere forever.
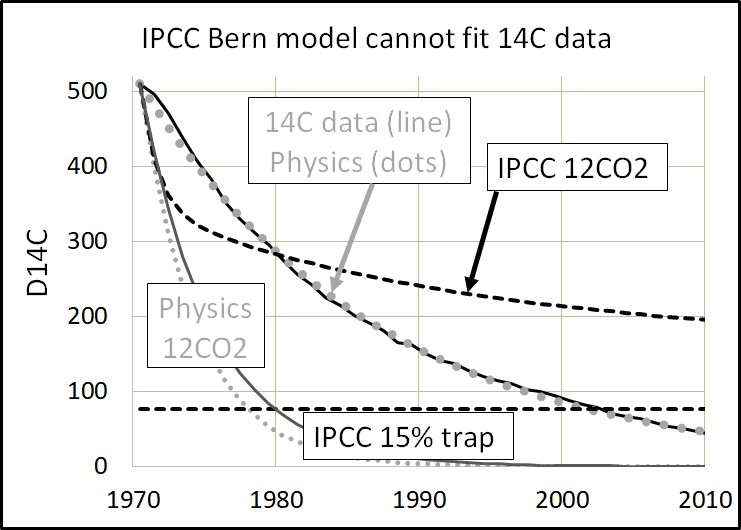
The IPCC Bern model is not just a failure to simulate data. The Bern model is a functional failure. It’s e-time increases significantly with time when 14C data show e-time is constant. The only way the Bern model can increase with time is by using its history as a reference.
Figure 10 shows how the IPCC Bern model cannot even replicate itself when it is restarted at any point in its simulation.
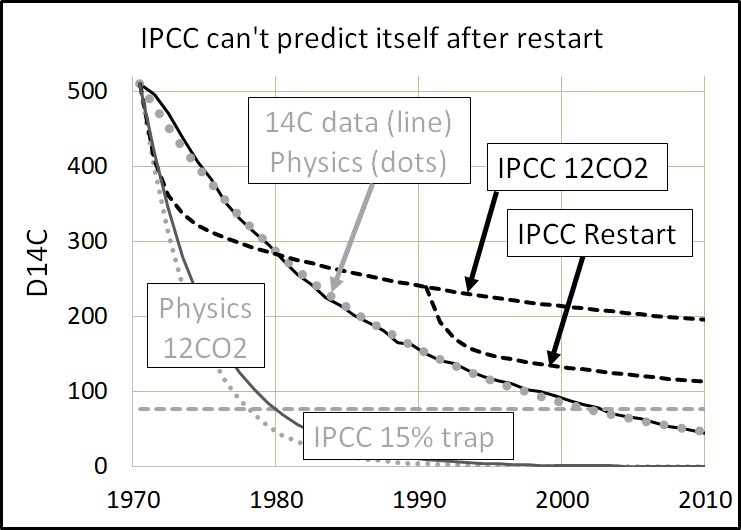
The IPCC Bern model cannot continue its same prediction line if it is restarted at any point. The Bern model cannot properly restart because it depends upon its history, which makes it an invalid model.
A restart deletes the Bern model’s history. This forces the Bern model to create a new history. In the real world, molecules do not remember their history. Molecules only know their present. Therefore, the IPCC Bern model fails the most basic test for a physical model.
Revelle and Suess [8] used 14C data to calculate correctly that human CO2 would increase atmospheric CO2 by only 1.2 percent as of 1957, based for an e-time of 5 years.
5.5 IPCC’s buffer theory is invalid
IPCC [3] claims:
The fraction of anthropogenic CO2 that is taken up by the ocean declines with increasing CO2 concentration, due to reduced buffer capacity of the carbonate system.
Buffer capacity is the ability of the oceans to absorb CO2.
Kohler et al. [7] claim human (but not natural) CO2 has reduced the “buffer capacity” of the carbonate system:
the rise in atmospheric and oceanic carbon content goes along with an increase in the Revelle factor, a phenomenon which is already measurable. This implies that the oceanic uptake of anthropogenic carbon will become slower if we continue to increase anthropogenic CO2 emissions. This is already seen in all CHIMP5 model simulations.
Kohler’s last sentence exhibits circular reasoning when it claims a model can prove what has been fed into the model.
All IPCC models use the buffer factor myth instead of Henry’s Law to conclude human CO2 causes all the rise in atmospheric CO2 [10].
The problem for Kohler and IPCC is data. Where are the data that support their claim? They have only their models. Models are not data. Models must make predictions that replicate data. Their models cannot replicate data.
Ballantyne et al. [38] found “there is no empirical evidence” that the ability of the land and oceans to absorb atmospheric CO2 “has started to diminish on the global scale.”
The 14C data are the most accurate way to measure changes in the Revelle factor and “buffer capacity.” Reduced buffer capacity, if it existed, would increase e-time. The 14C data prove e-time has been constant since 1970. Therefore, IPCC’s buffer capacity has been constant.
IPCC’s buffer capacity claim is absurd because it assumes only human CO2 reduces the buffer capacity while natural CO2 outflow does not. IPCC treats human and natural CO2 differently, which is impossible.
Kohler [7] claims lower buffer capacity affects only 12CO2, not 14CO2. That claim violates chemistry and physics. Segalstad [10] previously showed Kohler’s claim is impossible because “chemical and isotropic experiments show the equilibrium between CO2 and water is obtained within a few hours.”
The IPCC Bern model is based upon the invalid assumption that human CO2 decreases buffer capacity.
5.6 Isotope data support the Physics Model
IPCC [3] writes:
Third, the observed isotropic trends of 13C and 14C agree qualitatively with those expected due to the CO2 emissions from fossil fuels and the biosphere, and they are quantitatively consistent with results from carbon cycle modeling.
Human fossil-fuel CO2 is “14C-free” and the 14C balance level has decreased. IPCC [3] and Kohler [7] claim this proves human CO2 caused all the rise in atmospheric CO2.
But neither IPCC nor Kohler argue with numbers. Let’s do the calculations to compare the results from both models with the data. IPCC [2] says human CO2 comprises 32 percent of atmospheric CO2 while the Physics Model (12) says human CO2 is less than 5%. The question is whether the available isotope data support or reject either of the models.
RealClimate [39] says the 13C/12C ratio for human CO2 is about 98 percent of the ratio in natural CO2, and the 13C ratio has declined about 0.15 percent since 1850. RealClimate says this proves human CO2 caused all the increase in atmospheric CO2 since 1850.
Human CO2 causes the new balance level of D14C and 13C/12C to be:
Lb = Ln Rn + Lh Rh (15)
Where
Lb = the new balance level (of D14C or 13C/12C)
Ln = the natural balance level (D14C = 0; 13C/12C = 100%)
Lh = the human balance level (D14C = –1000; 13C/12C = 98%)
Rn = the fraction of natural CO2
Rh = the fraction of human CO2
The Physics Model predicts for D14C:
Lb = (0) (0.955) + (–1000) (0.045) = – 45 (16)
The IPCC model predicts for D14C:
Lb = (0) (0.68) + (–1000) (0.32) = – 320 (17)
The Physics Model predicts for 13C/12C:
Lb = (100) (0.955) + (98) (0.045) = 99.91 (18)
The IPCC model predicts for 13C/12C:
Lb = (100) (0.680) + (98) (0.320) = 99.36 (19)
The 14C data
The Physics Model (16) predicts human CO2 has lowered the balance level of 14C from zero to –45. The IPCC model (17) predicts human CO2 has lowered the 14C balance level to –320.
Figure 11 compares the Physics and IPCC predicted levels for human CO2 in the atmosphere.
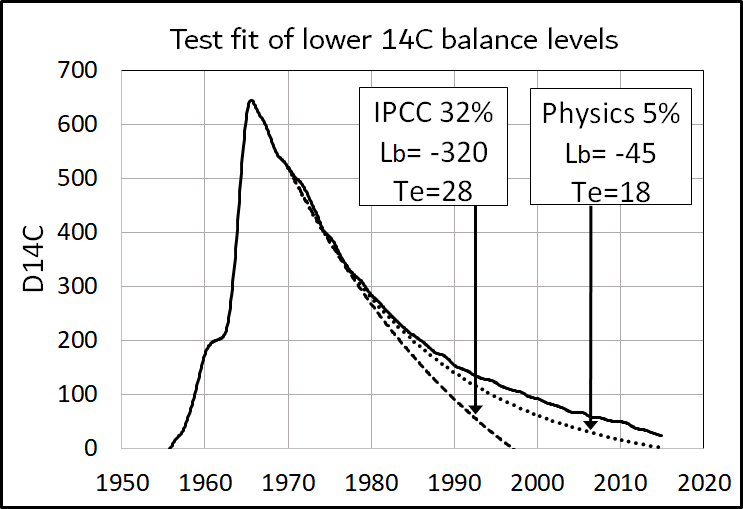
Figure 11 shows the Physics Model result of 5 percent human CO2 in the atmosphere matches the 14C data much better than the IPCC model of 32 percent of human CO2 in the atmosphere.
In summary, the 14C data support the Physics Model and reject the IPCC model.
The 13C data
The Physics Model (18) predicts human CO2 has lowered the 13C ratio by 0.09. The IPCC model (19) predicts human CO2 has lowered the 13C ratio by 0.64.
Figure 12 compares the Physics and IPCC predictions of the 13C/12C ratio to RealClimate’s numbers.
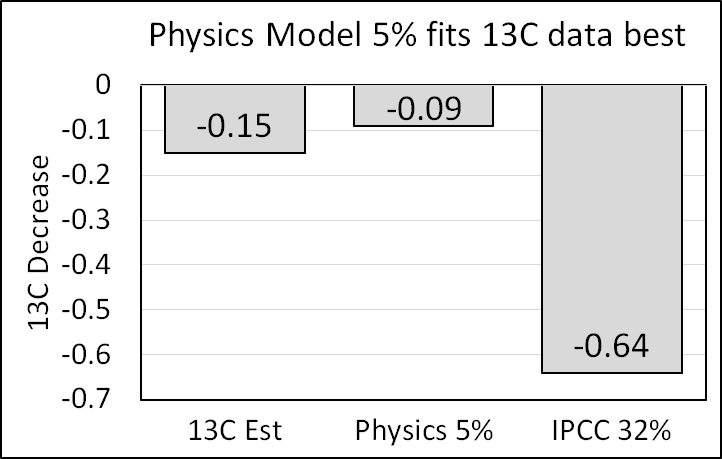
There seem to be no error bounds in the available 13C data. Nevertheless, even without error bounds the 13C data do not support the IPCC model over the Physics Model. So, the IPCC argument fails.
Segalstad [10] calculated similar results using permil units. He concluded the isotope data show human CO2 cannot be more than 4 percent of atmospheric CO2.
5.7 Mauna Loa data
Some scientists argue that a viable CO2 model must replicate the Mauna Loa CO2 data. The Physics Model can simulate the Mauna Loa data for atmospheric CO2.
Spencer [40] has a model that fits the Mauna Loa data. Spencer assumes like the IPCC that the natural level of CO2 is fixed at 280 ppm and human CO2 causes all the increase in atmospheric CO2. His model has many variables available to adjust so a fit to the Mauna Loa data is guaranteed. As von Neumann said [41] “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk.”
The significance of the fit by the Physics Model is that it comes with physical constraints that the other models do not have. The Physics Model e-time must be 4 years and natural CO2 must be 95 percent of atmospheric CO2.
Figure 13 shows how the Physics Model fits the Mauna Loa data.
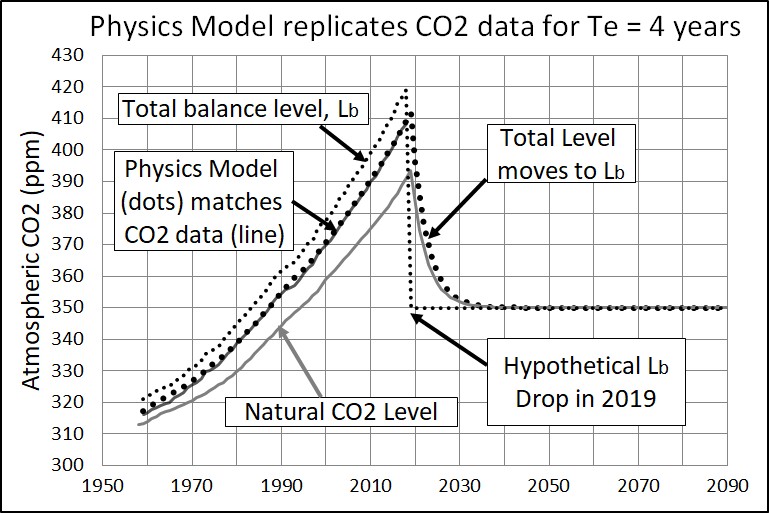
In Figure 14, the total balance level is the sum of natural and human balance levels. The balance level continues to rise. Level follows the balance level with a lag of about 4 years (the e-time), after the year 2000. This lag keeps the level about 10 ppm below the its balance level. Human CO2 adds to the natural level to produce the total level, about 15 ppm above the natural level.
In 2019, the balance level in Figure 14 is artificially reset to 350 ppm to test how fast the CO2 level moves to the new balance level. The total CO2 level falls to its new balance level of 350 ppm in about 10 years. No CO2 remains stuck in the atmosphere.
5.8 Ice-core data
IPCC claims “the observational CO2 records from ice cores … show that the maximum range of natural variability about the mean of 280 ppm during the past 1000 years was small.”
Using this invalid claim, IPCC assumes natural CO2 emissions remained constant within about one percent. IPCC’s invalid claim about ice-core data is the basis of IPCC’s invalid claim that human CO2 causes all the increase in atmospheric CO2 above 280 ppm. This increase is presently 130 ppm or 32 percent.
Siegenthaler and Joos [30] observed that ice-core data show natural CO2 increased by 17 ppm or 6 percent before 1900, when human CO2 emissions totaled only 5 ppm. These ice-core data contradict IPCC’s claim that natural CO2 emissions stayed constant after 1750.
Jaworoski [12] explains why ice-core data do not properly represent past atmospheric CO2. He concludes nature produces 97 percent of atmospheric CO2.
Proxy ice-core values for CO2 remained low for the past 650,000 years [10, 12]. If these ice-core values represent atmospheric CO2, then atmospheric CO2 did not cause any of the global warming in the last 650,000 years. And if CO2 did not cause global warming in the past, then the IPCC has lost its claim that CO2 causes present global warming [12].
Leaf stomata and chemical data prove the historical CO2 level was much higher than derived from ice cores [12]. There is no evidence that the pre-industrial CO2 level was 280 ppm as IPCC assumes.
Beck [13] reconstructed CO2 from chemical data show the level reached 440 ppm in 1820 and again in 1945.
IPCC’s claim that human CO2 produces all the increase in atmospheric CO2 above 280 ppm is invalid. In science, when data contradict a theory, the theory false. The IPCC, however, ignores how its theories contradict data.
6. Theories must be logical
6.1 IPCC’s response times fail physics
The Physics Model e-time has a precise definition: e-time is the time for the level to move (1 – 1/e) of the distance to its balance level.
Segalstad [10] observes IPCC [3] uses many definitions of lifetime — like residence time, transit time, response time, e-folding time, and adjustment time — in its quest to prove human CO2 remains in the atmosphere for hundreds of years. Many investigators, from 1957 to 1992, have calculated the e-time of atmospheric CO2 is about 5 years [10].
IPCC [3] defines “adjustment time (Ta)” as:
The time-scale characterising the decay of an instantaneous pulse input into the reservoir.
Cawley [5] defines “adjustment time (Ta)” as:
The time taken for the atmospheric CO2 concentration to substantially recover towards its original concentration following a perturbation.
The word “substantially” is imprecise.
Cawley follows IPCC to define “residence time (Tr)” as:
The average length of time a molecule of CO2 remains in the atmosphere before being taken up by the oceans or terrestrial biosphere.
Some authors use “residence time” to mean “e-time” but other authors, such as Cawley and IPCC, have a different meaning for residence time. This paper uses e-time because its definition is precise.
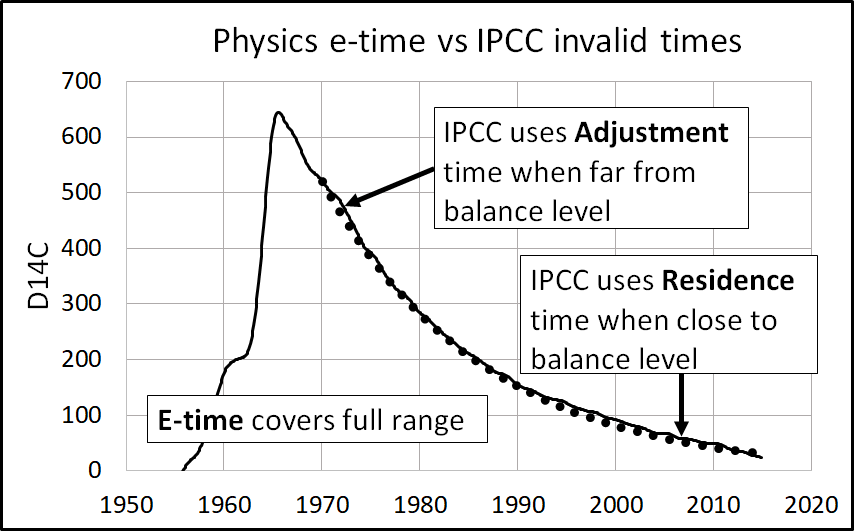
In summary, IPCC uses two different response times when it should use only e-time:
- When the level is far from its balance level (which can be zero), IPCC thinks e-time is an adjustment time because the level is moving rapidly toward its balance level.
- When the level is close to its balance level, IPCC thinks e-time is a residence time because “molecules” are flowing in and out with little change in level.
Figure 14 illustrates how e-time relates to IPCC’s adjustment and residence times.
IPCC defines “turnover time (Tt)” as:
The ratio of the mass M of a reservoir (e.g., a gaseous compound in the atmosphere) and the total rate of removal S from the reservoir: Tt = M/S.
IPCC’s turnover time seems to be the same as e-time except “removal” is not the same as outflow. Near the balance level, IPCC sometimes interprets “removal” to mean the difference between outflow and inflow.
IPCC says when outflow is proportional to level (the Physics Model hypothesis) then adjustment time equals turnover time. IPCC claims:
In simple cases, where the global removal of the compound is directly proportional to the total mass of the reservoir, the adjustment time equals the turnover time: Ta = Tt.
The Physics Model’s replication of the 14C data shows the 14CO2 outflow is proportional to level. Therefore, by IPCC’s own definition, adjustment time equals e-time equals residence time.
IPCC says in further confusion:
In more complicated cases, where several reservoirs are involved or where the removal is not proportional to the total mass, the equality T = Ta no longer holds.
Carbon dioxide is an extreme example. Its turnover time is only about 4 years because of the rapid exchange between atmosphere and the ocean and terrestrial biota.
Although an approximate value of 100 years may be given for the adjustment time of CO2 in the atmosphere, the actual adjustment is faster initially and slower later on.
IPCC agrees 12CO2 turnover time (e-time) is about 4 years. IPCC claims adjustment time is “fast initially and slower later on” which is why its Bern model cannot replicate the 14C data in Figure 9.
The 14C data show the e-time for 14CO2 is 16.5 years. This e-time is the upper bound for 12CO2 e-time. The IPCC claim of hundreds of years is based on IPCC’s misunderstanding of e-time.
Unfortunately, there are many different definitions of residence time. Therefore, this paper uses e-time with its exact definition.
6.2 IPCC’s first core argument is illogical
The IPCC [2] first core argument notes that human emissions from 1750 to 2013 totaled 185 ppm while atmospheric CO2 increased by only 117 ppm. These numbers are OK. But IPCC claims this proves human CO2 caused all the increase in atmospheric CO2 above 280 ppm. IPCC’s logic is faulty.
Figure 15 shows the IPCC first core argument.

 6.3 IPCC’s second core argument is illogical
6.3 IPCC’s second core argument is illogical
IPCC [2] claims nature has been a “net carbon sink” since 1750, so nature could not have caused the observed rise in atmospheric carbon dioxide. Please refer to Figure 5 that shows the inflow and outflow of atmospheric CO2.
Of course, nature is a “net carbon sink” because nature absorbs human CO2 emissions. However, absorption of human CO2 has no bearing whatsoever on how much natural CO2 flows into the atmosphere. Nature can set its inflow as it pleases, no matter how much human inflow nature absorbs. The 98-ppm natural flow can double or reduce to one-half while nature continues to absorb the outflow of the human addition to atmospheric CO2. So, the IPCC argument is absurd.
The Physics Model shows how CO2 inflows set balance levels in atmospheric CO2. At the balance level, outflow will equal inflow. No CO2 gets trapped in the atmosphere.
6.4 Key IPCC paper makes serious errors
Kohler [7] uses Cawley [5] to “prove” the IPCC case. But Cawley fails physics and statistics.
Cawley [5] is a key paper for the IPCC theory. Cawley claims human CO2 caused all the increase of atmospheric CO2 above the 280 ppm in 1750. But Cawley’s attempted proof fails physics.
Figure 17 shows three of Cawley’s equations.
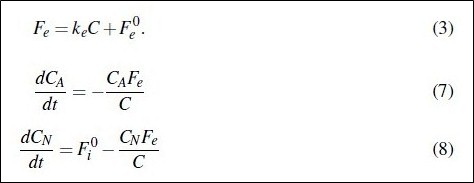
Cawley’s equation (3) attempts to do the same job as Physics Model (2), namely, to represent how level sets outflow. But Cawley adds to his equation (3) a second term that represents a steady-state outflow that is independent of level. Cawley’s added term is fictitious because his first term on the right side of his equation (3) is the true source of all outflow. As a result, all Cawley’s equations after his (3) are wrong, which makes his whole paper wrong.
Cawley’s equation (7) should include his Fa for human inflow. His equations (7) and (8) should omit his arbitrary Fe for outflow and set outflow equal to level (his C) divided by his residence time. His residence time is also inaccurate as shown in Section 6.1.
6.5 Statistical correlation
Cawley [5] argues,
Lastly, the rise in atmospheric carbon dioxide closely parallels the rise in anthropogenic emissions … which would be somewhat of a coincidence if the rise were essentially natural in origin!
IPCC [3] writes:
Second, the observed rate of CO2 increase closely parallels the accumulated emission trends from fossil fuel combustion and from land use changes.
IPCC incorrectly claims this proves human CO2 causes the increase in atmospheric CO2.
A standard scientific test for the non-existence of cause and effect is to show the correlation, of the assumed cause with the assumed effect, is zero.
For the IPCC to argue that human CO2 causes climate change, the IPCC must show that the correlation of human emissions with the increase in atmospheric CO2 is significantly greater than zero.
Proper statistics requires a detrended analysis of a time series to conclude cause and effect. Munshi [42] shows the “detrended correlation of annual emissions with annual changes in atmospheric CO2” is zero. Chaamjamal [43] extended Munshi’s calculations and found the correlations are zero for time intervals from one to five years.
Therefore, the standard statistical test for cause and effect proves human CO2 is insignificant to the increase in atmospheric CO2.
The ratio of annual change in atmospheric CO2 to annual human CO2 emissions that Munshi [42] tested is IPCC’s “airborne fraction”. Therefore, IPCC’s airborne fraction has no useful meaning.
An estimate of the airborne fraction is about 2.5 ppm/year divided by 5 ppm/year, or 0.5. Since the increase in level is caused by an increase in natural CO2 emissions, the airborne fraction has little physical meaning, and it would go to infinity if human emissions stopped.
Conclusions
The IPCC model and the Physics model compete to describe how human CO2 emissions add to atmospheric CO2. Both models agree that the CO2 inflow into the atmosphere is less than 5 percent human CO2 and more than 95 percent natural CO2.
The IPCC model concludes that human CO2 causes all the increase in atmospheric CO2 above 280 ppm; that 15 percent of all human CO2 emissions stays in the atmosphere forever; that 53 percent stays for hundreds of years; and only 32 percent flows freely out of the atmosphere like natural CO2.
The Physics Model treats human CO2 and natural CO2 the same because their CO2 molecules are identical. The Physics model makes only one hypothesis: CO2 outflow equals the level of CO2 in the atmosphere divided by e-time.
The Physics Model concludes that inflow sets a balance level equal to inflow multiplied by e-time, and that continuing inflow does not continue to increase atmospheric CO2. Rather inflow sets a balance level where outflow equals inflow and continuing inflow will not further increase the level of atmospheric CO2 beyond the balance level.
The proper test of two theories is not to claim the IPCC theory explains “observational evidence.” The proper test is the scientific method: if a prediction is wrong, the theory is wrong.
The 14C data following the cessation of the atomic bomb tests show how the level of CO2 in the atmosphere returns to its balance level after inflow decreases. All valid models of atmospheric CO2 must be able to replicate the 14C data.
The Physics Model exactly replicates the 14C data after 1970. This replication shows the e-time for 14CO2 is 16.5 years and that this e-time has been constant since 1970. The replication shows the Physics Model hypothesis — that outflow equals level divided by e-time — is correct.
The IPCC Bern model cannot replicate the 14C data. Its curve crosses the 14C data curve. The Bern model cannot even replicate itself if it is restarted at any point. This failure proves the IPCC Bern model does not have the mathematical structure for a valid model.
If natural CO2 is inserted into the Bern model, as physics requires, the Bern model predicts that 15 percent of natural CO2 inflow sticks in the atmosphere forever, which contradicts data and proves the Bern model is invalid.
The Physics Model concludes that the ratio of human to natural CO2 in the atmosphere equals the ratio of their inflows, independent of e-time, and that the e-times for both human and natural CO2 are the same. Using IPCC data, the e-time for 12CO2 is about 4 years.
The ratio conclusion means human CO2 adds only about 18 ppm and natural CO2 adds about 392 ppm to today’s CO2 level of 410 ppm. If all human CO2 emissions stopped and natural CO2 emissions stayed constant, then the level of atmospheric CO2 would fall only to 392 ppm in about 10 years. Nothing would be gained by stopping human CO2 emissions. There are no long-term effects of human CO2 emissions. Continued constant CO2 emissions do not add more CO2 to the atmosphere. Continued constant CO2 emissions simply maintain the balance level.
Acknowledgments
The author thanks Chuck Wiese, Laurence Gould, Tom Sheahen, Charles Camenzuli, and others who reviewed this paper and provided scientific critique and suggestions. The author thanks Daniel Nebert, Gordon Danielson, and Valerie Berry, who provided language and grammar suggestions.
This research did not receive any grant from funding agencies in the public, commercial, or not-for-profit sectors. This research was funded solely by the personal funds of the author.
Author’s contributions
The author declares he is the only contributor to the research in this paper.
Downloads
References
[1] USGCRP, 2017: Climate Science Special Report: Fourth National Climate Assessment, Volume I. U.S. Global Change Research Program, Washington, DC, USA, 470 pp; 2018. doi: 10.7930/J0J964J6. https://science2017.globalchange.gov/
[2] IPCC, 2001: Working Group 1: The scientific basis. The Carbon Cycle and Atmosphere CO2. https://www.ipcc.ch/site/assets/uploads/2018/02/TAR-03.pdf
[3] IPCC, 2007: Climate Change 2007: The Physical Science Basis. https://www.ipcc.ch/site/assets/uploads/2018/05/ar4_wg1_full_report-1.pdf
[4] D. Archer, M. Eby, V. Brovkin, A. Ridgwell, L. Cao, U. Mikolajewicz, et al., “Atmospheric Lifetime of Fossil Fuel Carbon Dioxide”. Annu. Rev. Earth Planet. Sci., 37, pp. 117–134; 2009. https://www.annualreviews.org/doi/pdf/10.1146/annurev.earth.031208.100206
[5] G.C. Cawley, “On the Atmospheric residence time of anthropogenically sourced CO2”. Energy Fuels 25, pp. 5503–5513; 2011. http://dx.doi.org/10.1021/ef200914u
[6] Z. Kern, M. Leuenberger, Comment on “The phase relation between atmospheric CO2 and global temperature” by Humlum et al. Glob. Planet. Change 100: 51–69.: Isotopes ignored. Glob. Planet. Chang. 109, 1–2; 2013. https://dx.doi.org/10.1016/j.gloplacha.2013.07.002
[7] P. Kohler, J. Hauck, C. Volker, D.A. Wolf-Gladrow, M. Butzin, J.B. Halpern, et al. Comment on “Scrutinizing the carbon cycle andCO2residence time in the atmosphere” by H. Harde, Global and Planetary Change; 2017. https://www.soest.hawaii.edu/oceanography/faculty/zeebe_files/Publications/KoehlerGPC17.pdf
[8] R. Revelle, H. Suess, “CO2 exchange between atmosphere and ocean and the question of an increase of atmospheric CO2 during past decades”. Tellus. 9: 18-27; 1957. http://onlinelibrary.wiley.com/doi/10.1111/j.2153-3490.1957.tb01849.x/abstract.
[9] C. Starr, “Atmospheric CO2 residence time and the carbon cycle”. Science Direct, 18, 12, pp. 1297-1310; 1992. https://www.sciencedirect.com/science/article/pii/0360544293900178
[10] T. V. Segalstad, “Carbon cycle modelling and the residence time of natural and anthropogenic atmospheric CO2: on the construction of the “Greenhouse Effect Global Warming” dogma”. In: Bate, R. (Ed.): Global warming: the continuing debate. ESEF, Cambridge, U.K. [ISBN 0952773422]: 184-219; 1998. http://www.co2web.info/ESEF3VO2.pdf
[11] Z. Jaworowski, “Climate Change: Incorrect information on pre-industrial CO2”. Statement written for the Hearing before the US Senate Committee on Commerce, Science, and Transportation. 2003. 2_Scandal.pdf”>https://21sci-tech.com/Articles%202007/20_1-2_CO2_Scandal.pdf
[13] E. Beck, “180 Years of Atmospheric CO2 Gas Analysis by Chemical Methods”. Energy & Environment. Vol 18, No. 2. 2007. https://journals.sagepub.com/doi/pdf/10.1260/0958305053749589
[15] R.S. Courtney, “Limits to existing quantitative understanding of past, present and future changes to atmospheric CO2 concentration”. International Conference on Climate Change, New York. 2008. https://www.heartland.org/multimedia/videos/richard-courtney-iccc1
[16] T, Quirk, “Sources and sinks of CO2”. Energy & Environment. Volume: 20 Issue: 1, pp. 105-121. 2009. https://journals.sagepub.com/doi/10.1260/095830509787689123
[17] R.E. Essenhigh, “Potential dependence of global warming on the residence time (RT) in the atmosphere of anthropogenically sourced CO2”. Energy Fuel 23, pp. 2773-2784; 2009. https://pubs.acs.org/doi/abs/10.1021/ef800581r
[18] J.A. Glassman, “On why CO2 is known not to have accumulated in the atmosphere and what is happening with CO2 in the modern era”. Rocket Scientist Journal; 2010. https://www.rocketscientistsjournal.com/2007/06/on_why_co2_is_known_not_to_hav.html#more
[19] M. L. Salby, “Physics of the Atmosphere and Climate”. Cambridge University Press. 2012. (ISBN: 978-0-521-76718-7) https://www.amazon.com/Physics-Atmosphere-Climate-Murry-Salby/dp/0521767180/ref=mt_hardcover?_encoding=UTF8&me=
[20] M. L. Salby, “Relationship Between Greenhouse Gases and Global Temperature”. Video Presentation, April 18, 2013. Helmut-Schmidt-University Hamburg. https://www.youtube.com/watch?v=2ROw_cDKwc0
[21] M. L. Salby, “Atmosphere Carbon”. Video Presentation, July 18, 2016. University College London. https://www.youtube.com/watch?v=3q-M_uYkpT0&feature=youtu.be
[22] M. L. Salby, “What is really behind the increase in atmospheric CO2?” Video Presentation, October 10, 2018. Helmut-Schmidt-University Hamburg, Germany. https://www.youtube.com/watch?time_continue=10&v=rohF6K2avtY
[23] O. Humlum, K. Stordahl, J.E. Solheim, “The phase relation between atmospheric CO2 and global temperatures”. Global and Planetary Change, 100, pp 51-69, 2013. https://www.sciencedirect.com/science/article/pii/S0921818112001658
[24] H. Harde, “Scrutinizing the carbon cycle and CO2 residence time in the atmosphere”. Global and Planetary Change. 152, 19-26; 2017. https://www.sciencedirect.com/science/article/pii/S0921818116304787. (https://edberry.com/wp-content/uploads/Climate/HardeHermann17-March6-CarbonCycle-ResidenceTime.pdf)
[25] H. Harde, “What Humans Contribute to Atmospheric CO2: Comparison of Carbon Cycle Models with Observations”. International Journal of Earth Sciences Vol. 8, No. 3, 2019, pp. x=x. doi: 10.11648/j.earth.20190803.xx http://article.esjournal.org/pdf/10.11648.j.earth.20190803.13.pdf
[26] E. X Berry, “A fatal flaw in global warming science”. Basic Science of a Changing Climate. Porto University, Portugal. Sep 7; 2018. https://www.portoconference2018.org/uploads/1/1/7/3/117342822/11_edwinberryportosep7final.pdf
[27] E. X Berry, “Contradictions to IPCC’s climate change theory”. Annual meeting of the American Meteorological Society, Phoenix; 2019. https://ams.confex.com/ams/2019Annual/meetingapp.cgi/Paper/349565
[28] T. Boden, B. Andres, (2017) Global CO2 emissions from fossil-fuel burning, cement manufacture, and gas flaring: 1751-2014. http://cdiac.ornl.gov/ftp/ndp030/global.1751_2014.ems.
[29] H. B. Dwight, “Tables of Integrals and Other Mathematical Data” Item 90.1. MacMillian Company; 1955. https://www.amazon.com/Tables-Integrals-Other-Mathematical-Data/dp/0023311703
[30] U. Siegenthaler, F. Joos, “Use of a simple model for studying oceanic tracer distributions and the global carbon cycle”. Tellus, 44B, 186-207; 1992. https://onlinelibrary.wiley.com/doi/10.1034/j.1600-0889.1992.t01-2-00003.x/epdf
[31] E. Maier-Reimer, L. Hasselmann, “Transport and storage of CO2 in the ocean – an inorganic ocean-circulation carbon cycle model”. Climate Dynamics 2(2):63–90; 1987. DOI: 10.1007/BF01054491
[32] F. Joos, R. Roth, J. S. Fuglestvedt, G. P. Peters, I. G. Enting, von Bloh, et al. “Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis”. Atmospheric Chemistry and Physics 13(5), doi: 10.5194/acpd-12-19799-2012. Atmos. Chem. Phys. 13, 2793-2825; 2013. https://www.atmos-chem-phys.net/13/2793/2013/acp-13-2793-2013.pdf
[33] F. Joos, “Parameters for tuning a simple carbon cycle model”. 2002. https://unfccc.int/resource/brazil/carbon.html
[34] Q. Hua, M. Barbetti, A. Z. Rakowski. “Atmospheric radiocarbon for the period 1950–2010”. RADIOCARBON, Vol 55, pp. 2059–2072. Table S2c. 2013. https://doi.org/10.2458/azu_js_rc.v55i2.16177
[35] J. C. Turnbull, S. E. Mikaloff Fletcher, I. Ansell, G. W. Brailsford, R. C. Moss, Norris, et al. “Sixty years of radiocarbon dioxide measurements at Wellington, New Zealand: 1954–2014”. Atmos. Chem. Phys., 17, pp. 14771–14784. 2017. https://doi.org/10.5194/acp-17-14771-2017
[36] I. Levin, T. Naegler, B. Kromer, M. Diehl, R. Francey, A. Gomez-Pelaez, et al., “Observations and modelling of the global distribution and long-term trend of atmospheric 14CO2”. Tellus B: Chemical and Physical Meteorology. 2010. https://www.tandfonline.com/doi/abs/10.1111/j.1600-0889.2009.00446.x
[37] Wikipedia: Isotopes. https://simple.m.wikipedia.org/wiki/Isotope
[38] A. P. Ballantyne, C. B. Alden, J. B. Miller, P. P. Tans, J. W. C. White, “Increase in observed net carbon dioxide uptake by land and oceans during the past 50 years”, Nature 488, pp. 70-73, 2012. doi:10.1038/nature11299. https://www.researchgate.net/publication/230615762_Increase_in_observed_net_carbon_dioxide_uptake_by_land_and_oceans_during_the_past_50_years
[39] RealClimate, “How do we know that recent CO2 increases are due to human activities?”. 2004. http://www.realclimate.org/index.php/archives/2004/12/how-do-we-know-that-recent-cosub2sub-increases-are-due-to-human-activities-updated/
[40] R. Spencer, “A simple model of the atmospheric CO2 budget”. 2019. http://www.drroyspencer.com/2019/04/a-simple-model-of-the-atmospheric-co2-budget/
[41] F. Dyson, “A meeting with Enrico Fermi”. Nature 427 (22 January 2004) p. 297. 2004. https://www.nature.com/articles/427297a
